Repurposing iterators as geometric generators

October 2021 (2679 Words, 15 Minutes)

c++ iterators generators computer vision backtracking

In this post, I’m going to cover a slightly unusual use case for custom C++ iterators. We are going to repurpose a C++ iterator as a generator to represent the geometric properties of circles and rectangles. This novel approach evolved while I was working on an interesting computer vision problem, and had a really nice effect on the memory footprint and program efficiency as you will soon see!

The problem

We’re given a basic black and white 2D scan of clothing buttons, and our job is to identify and highlight the broken buttons by placing a red box around them. We can easily understand how useful this would be on a factory production line to help automate quality control, so the motivation is clear.

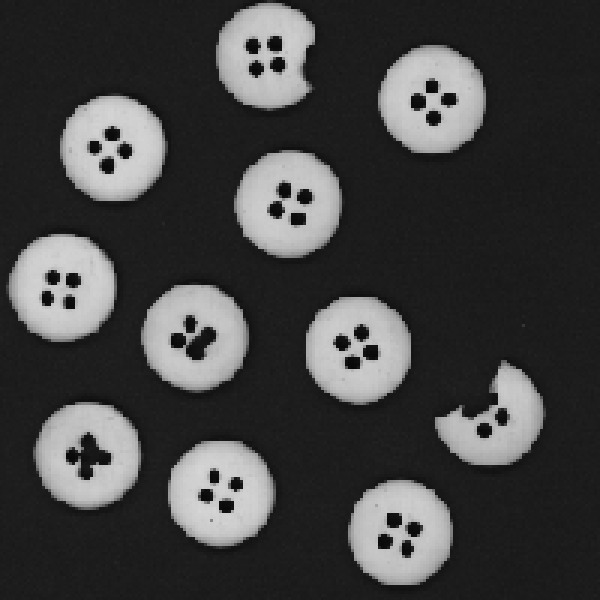
Scan of Buttons

We’re given the criteria for a button that passes the quality control test:

At the end of it all, we want to be able to highlight the broken buttons like so:

Highlighted Buttons

Use of Backtracking

We could make use of modern techniques to find the buttons, such as training a neural network, however using a backtracking algorithm is relatively simple and arguably quicker to implement.

Backtracking algorithms are very simple at their core but, as you probably already know, they start to get messy when we include predicate testing. Because we need to walk before we can run, we’re going to first identify the buttons and then move on to assessing their quality.

Finding the buttons

This is a pretty standard “finding islands within islands” problem, so I won’t go into detail about how we found the buttons (though if you’re curious, you can check out the full project on GitHub).

This is our working state once we’ve found all the buttons by their bounding boxes:

Found Buttons

Now we can move on to assessing them.

Assessing the buttons

Ignoring the number of holes requirement for now, we’ll first test for broken edges. As you can see from the scan, we need to take into account that buttons may not necessarily be the exact same size, color, or be perfectly round.

Since we know the bounds of each button, we can test for broken edges by taking advantage of good buttons being circular, with well-defined and known geometric properties. The scan is too pixelated to test buttons against a perfect circle, but we can test if they’re roughly circular. So given the origin and radius from the bounds, we can create two concentric circles and expect the button to fall somewhere between them.

Our two concentric circles will be slighty smaller and larger than the bounds:

const int radius =
  static_cast<int>(std::max(bounds.width(), bounds.height()) / 2.0f);

const Circle outer{bounds.center(), static_cast<int>(radius * 1.2f)};
const Circle inner{bounds.center(), static_cast<int>(radius * 0.9f)};
Code examples in this post have been simplified for clarity and may differ slightly from the final result found on GitHub.

To visualize this, we’ll draw the two concentric circles on the scan:

Concentric circles of test points

Our goal is to test that all points on the outer circumference are not part of the button, and all points on the inner circumference are part of the button.

Technically, a circle has an infinite number of points on its circumference, but that doesn’t translate well into code, so how do we test all points on its circumference?

Testing for “roughly circularness”

Our initial approach will be to first calculate the points on the circumference, then store them in a suitable data structure, and finally verify that each point satisfies the right condition.

Using Bresenham’s circle algorithm, we can generate a finite number of points on the circumference at fixed intervals for a single octant of a circle. These points can then simply be reflected across the x and y axes appropriately to generate the rest of the points in the other seven octants, as shown below:

Octants of a Circle

So now that we have our circumference points, we would ideally iterate over them and test each point against our condition:

  bool is_broken = std::any_of(circ.begin(), circ.end(), some_condition);
  // OR
  for (auto point : circ) {
    some_condition(point);
  }

There are a few problems with this approach:

  1. We need to store all of the circumference points in memory;
  2. We need to do this for both the inner and outer circumferences;
  3. We need to do this for every button.

You can see how this would quickly become a problem and very wasteful, especially if we’re processing a large number of buttons. So instead of storing all the points in memory, we’re going to create a custom iterator class called CircumferenceIterator and repurpose it as generator that will give us points on the circumference on-the-fly.

Custom iterators as generators

The CircumferenceIterator will function as you would normally expect a forward iterator to, but instead of returning the next point on the circumference by referencing it’s location in memory in some data structure, we will be generating it as the iterator is dereferenced. It’s a slightly out of the box idea, but I think the results will speak for themselves!

We don’t need to do anything out of the ordinary to define our custom iterator. We only need to add the usual (C++17) iterator traits and begin() and end() so it will play nice with STL algorithms that work on std::ranges.

Given a specific Circle instance, we create a CircumferenceIterator such that we have access to the geometric properties of the circle needed to generate the next point on the circumference:

  /**
    * @brief Construct a CircumferenceIterator for a given Circle.
    *
    * @param c The Circle to generate points for.
    * @param dx The x coordinate of the first point on the circumference.
    */
  constexpr CircumferenceIterator(Circle const &c, int dx) noexcept
      : circle{c}, dx{dx}, radius{c.get_radius()},
        origin_x{c.get_origin().get_x()}, origin_y{c.get_origin().get_y()} {};

You may have been thinking, “why not calculate the position of a point on the circumference and then immediately assess it?”, and you’d be right! That’s exactly what repurposing an iterator as a generator will allow us to do, and we’re going to do it in a way that’s more efficient and readable than the naïve approach above.

A first pass with the first octant

For our CircumferenceIterator to act as a generator, we need to customize the dereference and increment operators while keeping track of the current octant at the class instance level. The dereference operator will do most of the heavy lifting—it will return the next point taking the current octant into account.

Here’s what it would look like if we were only generating points for one octant using Bresenham’s circle algorithm:

/**
  * @brief Dereferences the iterator to get the current point on the circumference.
  */
Point CircumferenceIterator::operator*() const {
  const int dy = (int)sqrt(pow(radius, 2) - pow(dx, 2));

  return Point{origin_x + dx, origin_y + dy};
}

/**
  * @brief Increment the iterator to the next point on the circumference.
  */
CircumferenceIterator CircumferenceIterator::operator++() {
  dx += 1;

  return *this;
}

CircumferenceIterator CircumferenceIterator::begin() const {
  return CircumferenceIterator{circle, 0};
}

CircumferenceIterator CircumferenceIterator::end() const {
  const int end_dx = static_cast<int>(circle.get_radius() / sqrt(2) + 1);

  return CircumferenceIterator{circle, end_dx};
}

Which would result in the following:

One Octant

Jumping from octant to octant

Naturally, our first approach would involve testing all points in one octant to completion before moving on to the next, but instead we’re going to calculate all the reflected points for the current x coordinate in all eight octants before moving on. Here’s what that would look like if we drew the points as we moved around:

All Octants

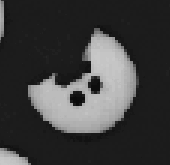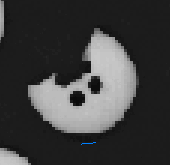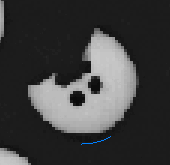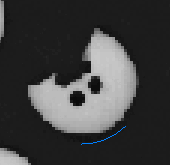
Doing this has a neat effect on efficiency! Keeping our goal in mind to find the broken buttons, we want to stop as soon as we find any point that doesn’t satisfy the tested condition. We can test more effectively by jumping from octant to octant and covering a larger area of the button in a shorter amount of time. It’s easy to see where the increase in speed comes from with broken buttons like the one above.

Taking all eight octants into account, our dereference and increment operators now look like this:

Point CircumferenceIterator::operator*() const {
  const int dy = (int)sqrt(pow(r, 2) - pow(dx, 2));

  switch (octant) {
  case 0: return Point{origin_x + dx, origin_y + dy};
  case 1: return Point{origin_x + dx, origin_y - dy};
  case 2: return Point{origin_x - dx, origin_y + dy};
  case 3: return Point{origin_x - dx, origin_y - dy};
  case 4: return Point{origin_x + dy, origin_y + dx};
  case 5: return Point{origin_x + dy, origin_y - dx};
  case 6: return Point{origin_x - dy, origin_y + dx};
  case 7: return Point{origin_x - dy, origin_y - dx};
  default: assert(false); // Impossible situation
  }
}

CircumferenceIterator CircumferenceIterator::operator++() {
  if ((++octant %= 8) == 0) ++dx;

  return *this;
}

// begin() and end() remain the same

Now we get to the cool part, seeing how it all comes together!

Plugging into STL algorithms

It turns out that representing a geometric property like the points on a circumference with an iterator-turned-generator works quite well! We can now plug straight into STL algorithms, and most importantly keep our backtracking algorithms succinct and avoid cluttering them with our bad button tests.

Checking that each button is roughly circular is now very succinct and fantastically readable thanks to std::any_of and a few predicate functions:

// For each found button:
bool is_broken = false;

// Test the points on the outer circumference.
is_broken |= std::any_of(outer_circumference.begin(), outer_circumference.end(),
                         is_part_of_fastener);

// Test the points on the inner circumference.
is_broken |= std::any_of(inner_circumference.begin(), inner_circumference.end(),
                         is_not_part_of_fastener);

Now coming back to the requirement for the number of button holes, we’ll use another backtracking algorithm to locate the interior holes of each button and check that against our requirements:

// For each found button:
bool is_broken = false;

// Test the concentric circles...

is_broken |= discover_num_holes(inner.bounding_box()) != kNumRequiredHoles;

Below shows each hole that the backtracking algorithm discovered:

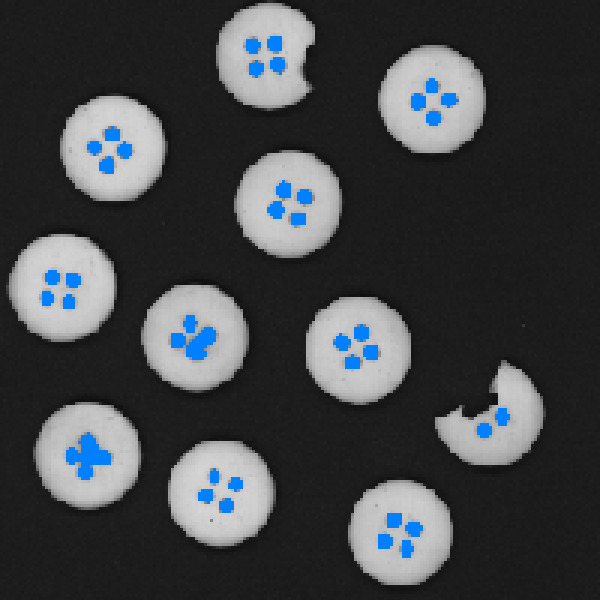
Button Holes Backtracking

Now that we can accurately distinguish good buttons from bad buttons, we’ll want to add a box around them to highlight the bad ones. Our custom iterator doesn’t just work for circles though, we can apply the same concepts as above to the perimeter of rectangles too! We’ll accomplish this by creating a PerimiterIterator for the bounding box, and with the appropriate changes to the dereference and increment operators, we can do the following:

if (is_broken) {
  for (auto const &point : bounds.perimeter()) draw_point(point, Color::Red());
}

And here’s a visualization of all of our hard work coming together:

Result

The outcome

This was just a small part of the larger project of many classes and multiple namespaces! Like I mentioned before, backtracking algorithms are very simple at their core, and they usually get complicated when they’re riddled with tests. This was going to be especially true, considering we are performing backtracking within backtracking! With around 100 lines of code, we managed to reduce the overall complexity of our algorithms and bring some clarity to what we’re doing.

Although it’s a not a conventional application for an iterator, I thought it was novel enough to be worth sharing! With a bit of out-of-the-box thinking, we were able to represent geometric properties by building iterators from primitives that plug straight into STL algorithms, and create fantastically readable code that expresses succinctly what we were trying to achieve.

Below is the culmination of our work in this post in the function to process a scan. I’d highly recommend checking out the entire project to fully appreciate the approach!

void alg::process_scan() {
  for (auto const &bounds : discover_all_button_bounds()) {
    bool is_broken = false;

    // Draw two concentric circles and require that the pixelated edge of the
    // button falls between them.
    const int radius =
        static_cast<int>(std::max(bounds.width(), bounds.height()) / 2.0);

    const geom::Circle outer{bounds.center(), static_cast<int>(radius * 1.2)};
    const geom::Circle inner{bounds.center(), static_cast<int>(radius * 0.9)};

    auto outer_circumference = outer.circumference();
    auto inner_circumference = inner.circumference();

    is_broken |= std::any_of(outer_circumference.begin(),
                             outer_circumference.end(),
                             is_part_of_fastener);

    is_broken |= std::any_of(inner_circumference.begin(),
                             inner_circumference.end(),
                             is_not_part_of_fastener);

    is_broken |= discover_num_holes(inner.bounding_box()) != kNumRequiredHoles;

    if (is_broken) {
      for (auto const &point : bounds.perimeter())
        draw_point(point, Color::Red());
    }
  }
}
Check out the repo on GitHub!
© 2024 Tessa Power   •  Theme  Moonwalk